This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Evan Ning, Milton Academy & [email protected];
(2) David R. Kaeli, Department of Electrical and Computer Engineering & Northeastern University [email protected].
Table of Links
- Introduction
- Sieve Optimizations
- Mathematical Optimization
- Implementation
- Results and Discussions
- Conclusions, Source Code & References
5. Results and Discussions
Our Sieve algorithm implementation uses the POSIX threads C++ libraries [7]. The performance study was carried out on the system described in Table 2. By leveraging a high-performance computing cluster, our implementation aims not just to sieve primes efficiently, but to push the boundaries of what's possible in large-scale prime enumeration.

The computation time is measured while varying the number of threads and the value N, which specifies the range that we are sieving to. The memory usage is 1,000,000 x 4B x 2 = 8MB for the two A_one and A_five arrays.
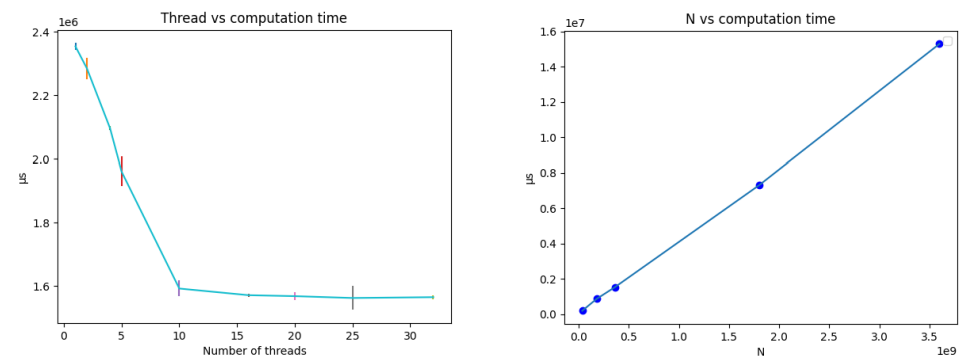
Inspect the graph on the left, the computation time drops linearly against the number of threads until thread number = 10. In the right graph, we can see the linear correlation between the value of N and computation time. The result shows that our algorithm is highly scalable.
The interplay between memory size and computational speed is a pivotal aspect of algorithm optimization. Our second set of experiments delved deeper by exploring how the sizes of the A_one and A_five arrays, which serve as the scratch memory during each thread's operations, influence the algorithm's overall performance. When the sizes of the scratch memory arrays increased, the number of iterations the program needs to complete its task decreased. Using a larger memory pool, more prime sieving results can be held at once, enabling more extensive sieving in a single pass. Thus, fewer passes or iterations are required to achieve the end goal. Our experiments ranged from using a tiny scratch memory size of 100k, suitable for environments with stringent memory restrictions, to a spacious 100M, tailored for systems where memory is abundant. The goal was to find a balance - a size that minimizes the iteration count, while also being mindful of memory usage constraints.
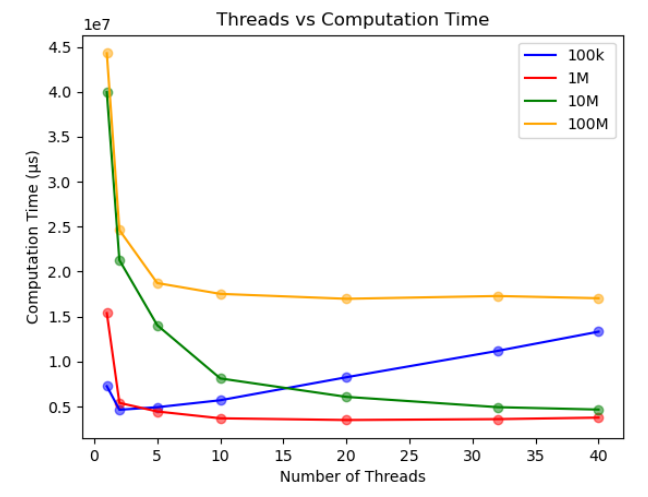
The results from these experiments have shown some very interesting findings. At first glance, one might assume that a scratch memory size of 100M, the largest in our experiments, would achieve the best performance in terms of computation time. However, the performance was poor when using this configuration. We believe it is an attribute of the intrinsic memory constraints of what the parallel node can allocate efficiently. When the memory exceeds this limit, the operating system swaps pages, which is causing significant delays. This swapping of memory pages between the RAM and the disk is notoriously slow, introducing significant delays in execution. Hence, while having a large scratch memory may reduce iterations, the overheads introduced due to page swapping can negate those benefits.
For the 100k array size, where each thread uses the least amount of memory, we ran into different challenges. The execution time grew as the number of threads increased, an anomaly unique to this configuration. A higher thread count implies that each thread's designated segment shrinks. When these segments approach, or dip below, the size of a cache line, cache synchronization becomes mandatory among threads. This synchronization can lead to stalls, as cache lines are evicted and fetched repeatedly, impacting performance.
The best performance is achieved by 1M array size, as this amount of scratch memory can avoid cache collisions and page swapping. Overall, the cache and memory play a significant role in the overall performance. Choosing the right scratch memory size is a critical parameter to achieve good multithread performance.

