This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Xiaoyu Ai, School of Electrical Engineering & Telecommunications, University of New South Wales, Sydney, NSW 2052, Australia;
(2) Robert Malaney, School of Electrical Engineering & Telecommunications, University of New South Wales, Sydney, NSW 2052, Australia.
Table of Links
- Abstract & Introduction
- System Overview
- Overcoming the limitation of key reconciliation
- Final Key Rate
- Experimental Results
- Discussion
- Conclusion & References
- Appendix
V. EXPERIMENTAL RESULTS

A. Decoding Error and Time

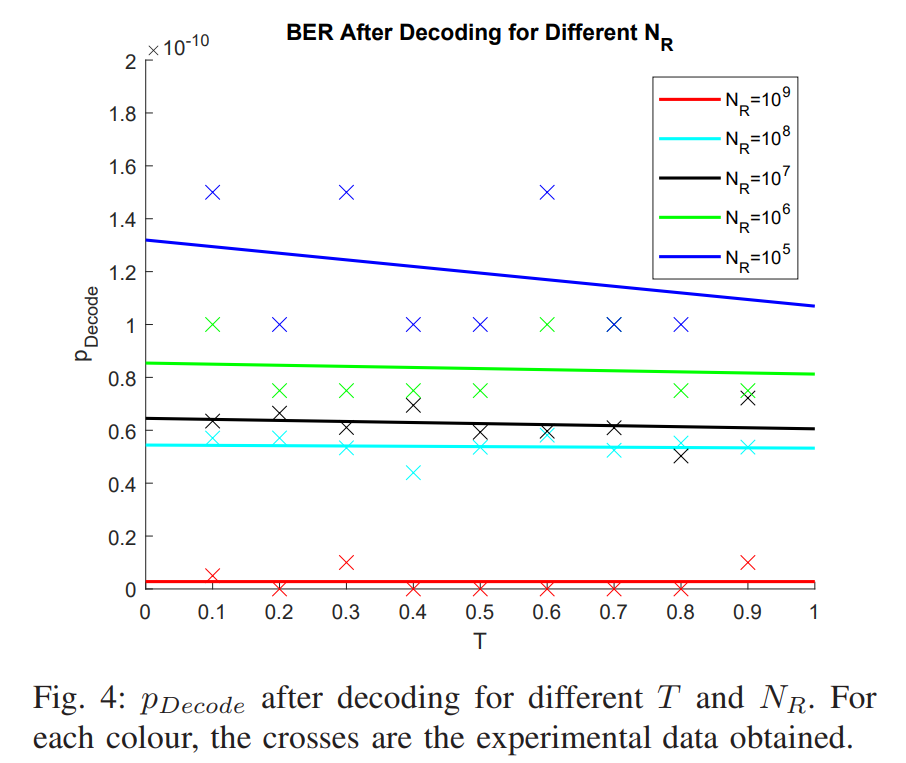
B. The Optimal NR

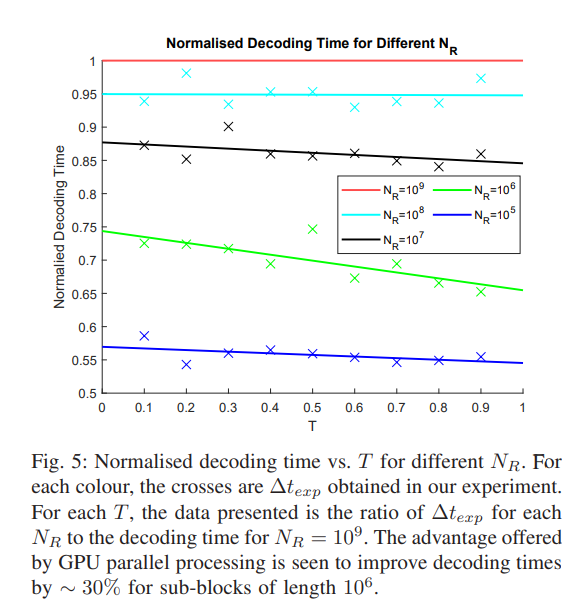
For this experiment, we pre-built a database to store LDPC codes with their code rates ranging from 0.01 to 0.8 and their block lengths ranging from 106 to 109 . For code rates less than 0.1, Multi-Edge-Type LDPC codes (degree distributions outlined in [22]) were used. These achieve a lower pDecode compared to irregular LDPC codes with the same code rate. For code rates greater than or equal to 0.1, we adopted the irregular LDPC codes (degree distributions outlined in [57]). At such code rates, these latter codes have the same pDecode performance as the Multi-Edge-Type counterparts, but allow for faster code construction.

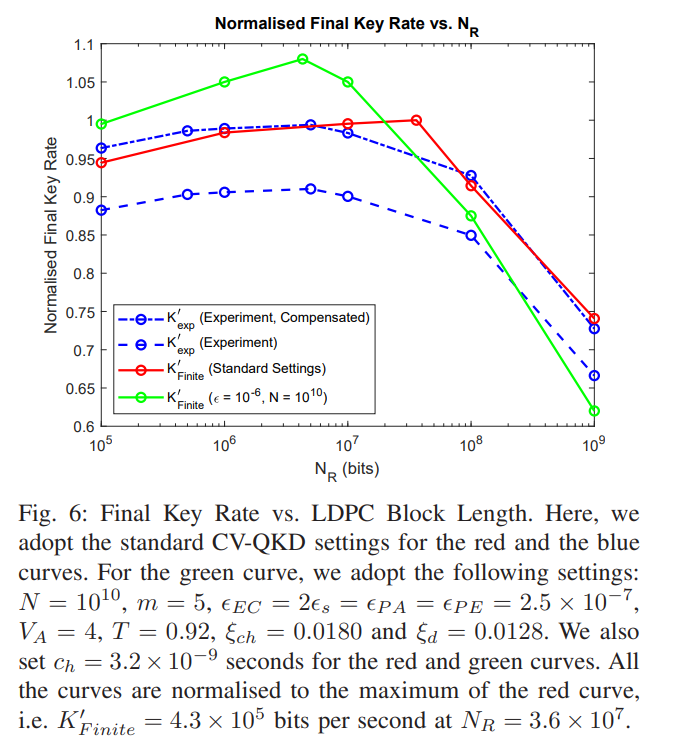


C. Final-key Effect for a Given No
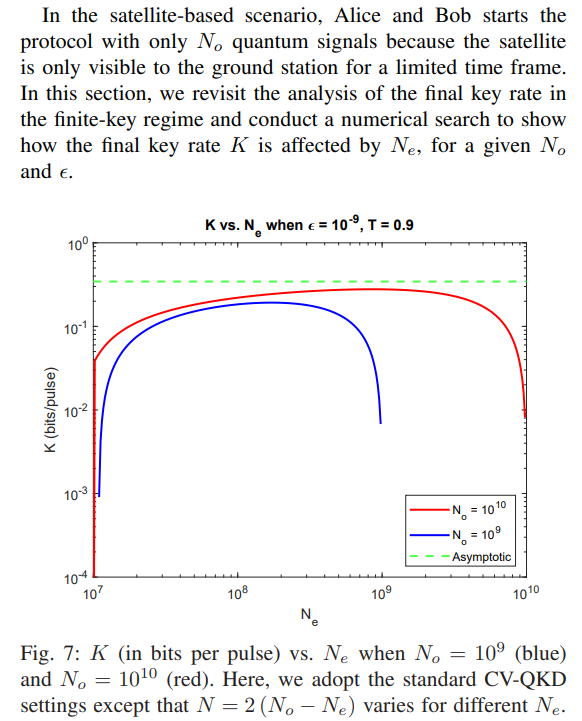

[15] Recall, we are particularly interested in the satellite-to-Earth channel. As in other works, we assume losses for this channel are dominated by diffraction effects, and therefore the transmissivity can be held constant. We further assume post-selections, using a bright classical beam sent along with the quantum signals (but different polarisation), remove any significant transmissivity deviations. As discussed elsewhere [17], some receiver/transmitter apertures, coupled to detailed phase-screen simulations of satellite downlink channels, render the constant-transmissivity assumption reasonable [56]. If the transmissivity is highly variable the optimal block length, NR, can be calculated by an expectation over the transmissivity density function.
[16] We adopted the following method to determine ch. For m LDPC codes with NR = 106 and T = 0.9, we obtained the total number of arithmetic operations for those codes. Next, we measured the elapsed time to reconcile a block of 106 quadrature values. We then obtained ch by dividing the number of arithmetic operations to this measured elapsed time.
[17] These trapping sets are the primary reason that additional decoding iterations are consumed for only a marginal decrease of the decoding error, i.e. the error floor effect [58].

