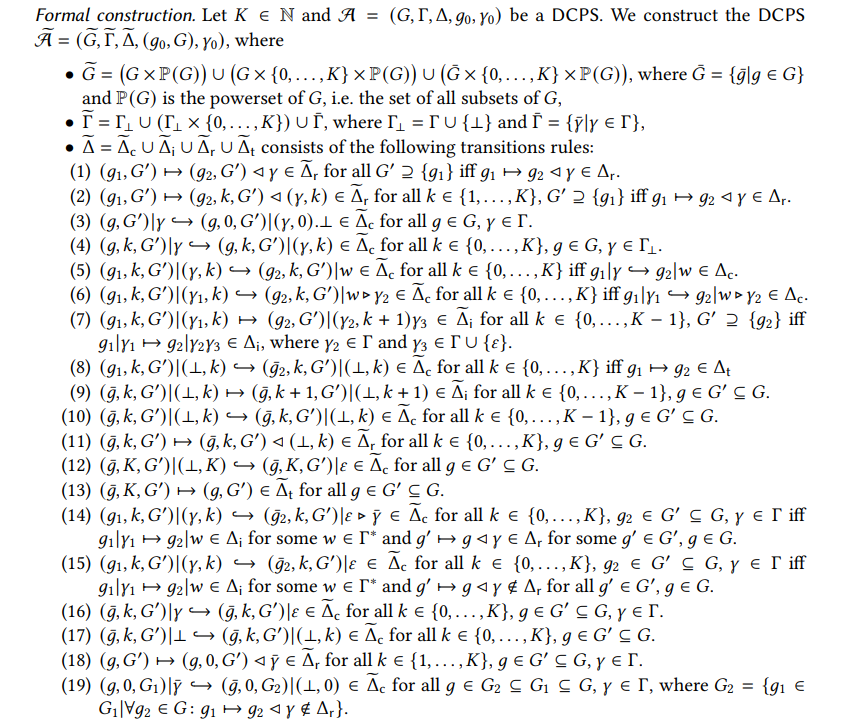This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.
Authors:
(1) Pascal Baumann, Max Planck Institute for Software Systems (MPI-SWS), Germany;
(2) Rupak Majumdar, Max Planck Institute for Software Systems (MPI-SWS), Germany;
(3) Ramanathan S. Thinniyam, Max Planck Institute for Software Systems (MPI-SWS), Germany;
(4) Georg Zetzsche, Max Planck Institute for Software Systems (MPI-SWS), Germany.
Table of Links
- Introduction
- Dynamic Networks of Concurret Pushdown Systems (DCPS)
- Warm-up: Non-Termination
- Fair Non-Termination
- From Progressive Runs for VASSB to Reachability
- Starvation
- Conclusion, Acknowledgment & References
- A. Strengthening Fairness to Progressive Runs
- B. Proofs from Section 4.1
- C. Proofs for Section 5
- D. Proofs for Section 5.3
- E. Proofs for Section 6
A STRENGTHENING FAIRNESS TO PROGRESSIVE RUNS
In this section we strengthen the notion of fairness for DCPS to progressiveness by proving Lemma 4.3.
Idea. To prove Lemma 4.3 we modify the DCPS A by giving every thread a bottom of stack symbol ⊥ and saving its context switch number in its top of stack symbol. We also save this number in the global state whenever a thread is active. This way we can still swap a thread out and back in again once it has emptied its stack, and we also can keep track of how often we need to repeat that, before we reach K context switches and allow it to terminate.
Furthermore, we also keep a subset A ′ of the global states of A in our new global states, which restricts the states that can appear when no thread is active. This way we can guess that a thread will be “stuck” in the future, upon which we terminate it instead (going up to K context switches first) and also spawn a new thread keeping track of its top of stack symbol in the bag. Then later we restrict the subset G ′ to only those global states that do not have Resume rules for the top of stack symbols we saved in the bag. This then verifies our guess of “being stuck”.