This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Xiaoyu Ai, School of Electrical Engineering & Telecommunications, University of New South Wales, Sydney, NSW 2052, Australia;
(2) Robert Malaney, School of Electrical Engineering & Telecommunications, University of New South Wales, Sydney, NSW 2052, Australia.
Table of Links
- Abstract & Introduction
- System Overview
- Overcoming the limitation of key reconciliation
- Final Key Rate
- Experimental Results
- Discussion
- Conclusion & References
- Appendix
IV. FINAL KEY RATE
We now present the penalty incurred for the division of N in the finite-key regime, and then propose an optimisation procedure to find the optimal NR which maximises the final key rate in bits per second.
A. Analysis of the Final Key Rate
For the protocol considered, in the finite-key regime the final key rate in bits per pulse, K, under the assumption of Gaussian collective attacks is adopted as [28], [49], [50][11]

Thus far, we have been analysing the final key rate in bits per pulse. However, the final key rate in bits per second is more interesting in our context - the system will not be viable if the reconciliation takes too long to complete. From this point forward, we use a dashed symbol to distinguish a final key rate that is given in bits per second. Taking the decoding complexity into account, and ignoring the time taken to acquire the quantum signals, we can write the final key rate, K′ Finite, as
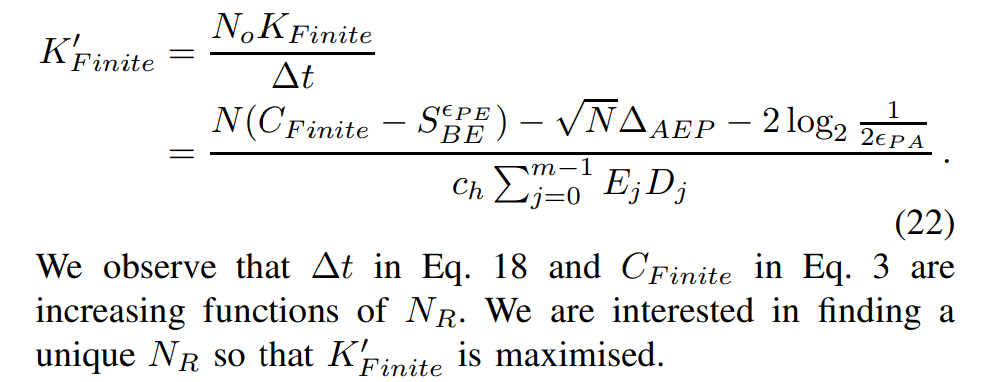
B. Optimised LDPC Blocklength for CV-QKD Reconciliation

where

Eq. 30 can be solved via a numerical root-finding algorithm [54]. If we consider the standard CV-QKD settings, we obtain a stationary point at NR = 3.6×107 bits (the value of K′ Finite at this NR is discussed later).

[11] This key-rate formulation was developed in [49] with a typographical error corrected in [50]. Eq. 19 is from [28] which acknowledged the correction and simplified the final key rate formulation (see footnote 2 of [51] for more details). A general discussion on the use of other key-rate formulations (e.g. [52], [53]) within our framework is given later.
[12] Recalling Eq. 18, we note that for a given LDPC code, Ej is only dependent on the degree distribution pairs and Dj is only a function of the degree distribution pairs and γ.
[13] In using this technique it is important to check that the inequality holds for the chosen parameter range of interest. This is done for all calculations we show here, but also for a much wider range not shown. For example, we find for ǫ = 10−9 , N = 109 and m = 5, the inequality 28 holds for any combination of the remaining parameters selected from the ranges VA ∈ [1, 34], T ∈ [0, 1] and ξ = [0, 0.05].
[14] The values of ξch and ξd in the standard CV-QKD settings are predicted values after accounting for all noise terms [17].

