This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Xiaoyu Ai, School of Electrical Engineering & Telecommunications, University of New South Wales, Sydney, NSW 2052, Australia;
(2) Robert Malaney, School of Electrical Engineering & Telecommunications, University of New South Wales, Sydney, NSW 2052, Australia.
Table of Links
- Abstract & Introduction
- System Overview
- Overcoming the limitation of key reconciliation
- Final Key Rate
- Experimental Results
- Discussion
- Conclusion & References
- Appendix
II. SYSTEM OVERVIEW
Although, as just stated, our analysis will apply to most CV-QKD protocols, for detailed quantitative discussion we will consider only one specific CV-QKD protocol - the “noswitching” protocol [27]–[29] based on heterodyne detection. In this protocol, the quantum signal is encoded using Gaussian-modulated coherent states [27]. The main advantage of the no-switching protocol is that Alice and Bob can utlise all measurement results [28] (in most other protocols some results are discarded due to a random quadrature selection). We also adopt a Slice Reconciliation (SR) variant named Multi-Stage Hard Decoding[4] (MSHD) [30], [33], [34] for the classical reconciliation step, where the number of bits derived from each measurement outcome is m. We refer to this variant simply as SR in the following.
It is worth noting that the optimisation analysis to follow is to some extent independent of the details of the reconciliation scheme. However, SR [30], [36] can be compared with the other well-known reconciliation scheme for CV-QKD - multidimensional reconciliation [37]. It is known that SR achieves higher reconciliation efficiency when the Signal-to-Noise Ratio (SNR) is greater than 1 [36]. At low SNR the opposite is true. For focus, here we adopt SR (as multistage hard decoding [36]) since in many satellite scenarios post-selection is used to filter out the low SNR quantum signals [1]. Our adopted scheme will be more useful in such scenarios.
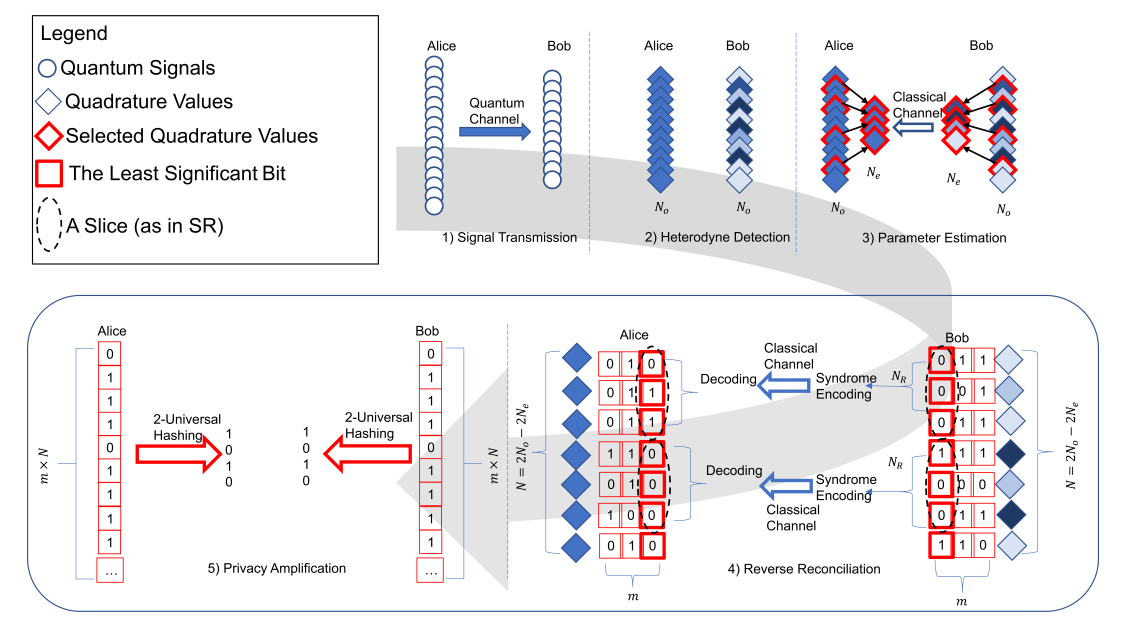
We now briefly describe the steps of the protocol, a diagram of which shown in Fig. 1. In the following, we assume the quantum signalling rate is much larger than the reconciliation rate.
• Step 1: Signal Preparation. Alice selects a fixed modulation variance VA. For each quantum signal to be transmitted to Bob, Alice randomly selects a number from a Gaussian distribution, N(0, VA), and then prepares a signal by displacing one of the quadrature components of a vacuum state by this random number. The process is repeated on the signal for the other quadrature. The signal is then transmitted to Bob.
• Step 2: Heterodyne Detection. Bob performs heterodyne detection to obtain the two quadrature values (real numbers) for each received signal. Bob compares each measured quantum signal with a given cut-off threshold and informs Alice to discard her corresponding quantum signal if his measured quantum signal is lower than the threshold[5] . A quantum signal that is lost in transit registers a null signal at Bob. Neglecting null signals, Bob holds 2No quadrature values at the end of this process.
• Step 3: Parameter Estimation. Bob randomly selects a subset 2Ne from the 2No quadrature values and sends this estimation subset, along with the corresponding time information, to Alice via classical communications (we adopt Ne = 1 2No, unless otherwise stated). Alice uses the timing information to best pair the signals in this subset (and therefore the corresponding quadrature values) sent by her and then estimates the covariance matrix between the shared states. Based on the estimated covariance matrix, Alice determines the channel transmissivity, T , excess noise, ξ, Bob’s SNR, γ, the Holevo Information, χBE, between Bob and the eavesdropper (Eve), and the mutual information between Alice and Bob, IAB. Finally, for a given target reconciliation efficiency β, Alice compares χBE with βIAB. Alice aborts the protocol if χBE ≥ βIAB. Otherwise, Alice informs Bob of the estimation results, i.e. T , ξ, γ, χBE and IAB.
• Step 4: Bit Error Estimation for SR. Using Gray Labelling, Alice and Bob represent each of the quadrature values embedded in each signal with m bits. Then, for quadrature values selected in the estimation subset, Alice forms a Ne-by-m bit matrix and Bob does the same. Next, Alice and Bob exchange their matrices and compare the j th column of the two matrices to estimate the Bit Error Ratio[6] (BER), pj , j ∈ {0, 1, · · · , m−1}, for all the digits in the j th column. The estimated pj will be used in SR. Finally, Alice and Bob discard all the quadrature values in the estimation subset. At the end of this step, Alice and Bob each hold a mN-bit string.
• Step 5: Reverse Reconciliation. For each column, Alice and Bob agree on an LDPC code with block length NR that is closest to the capacity determined by pj. Bob forms a new NR-bit string (referred as a “slice” in SR) by selecting the j th digit (bit) of each of the NR quadrature values, encodes the new bit string (the slice) into syndrome bits, and sends those bits to Alice (see III.B for details). Alice then initiates SR to obtain her best estimate of Bob’s string. Alice repeats this process until all her mN bits are reconciled. Finally, Alice and Bob obtain two hashed strings by applying the same hash function to their reconciled strings and exchange the hash results to check whether SR is successful. If successful, Alice holds a mN-bit string identical to Bob’s mN-bit string. Otherwise, they abort the protocol and restart from Step 1.
• Step 6: Privacy Amplification. Based on Eq. 19, Alice and Bob compute the length of the secret key that can be extracted and then apply a 2-universal hashing function on their reconciled string to obtain two identical and shorter secret key strings about which Eve has effectively no knowledge.
[4] The slice reconciliation can be implemented with 2 other variants: Bit Interleaved Coded Modulation (BICM) [30] and Multi-Level Coding/MultiStage Decoding (MLC/MSD) [31], [32]. We note that the MLC/MSD takes advantage of the dependence between slices to select the optimal LDPC code rates [30], [32]. However, as a special case of MLC/MSD, MSHD assumes that the slices are independent [30], [33], [34]. Using MSHD leads to a tractable analysis at the expense of sub-optimal selection of LDPC code rates, but such expense is negligible if Gray Labelling [35] is adopted and the number of slices is at least 5 [30], [34], as is the case in this work.
[5] The Gaussian post-selection technique at Bob’s side effectively improves the channel conditions between Alice and Bob [38] so that SR is preferred for reconciliation (rather than multidimensional reconciliation).
[6] At this step, sources of bit errors include the channel transmission, heterodyne detection, and quantisation.

